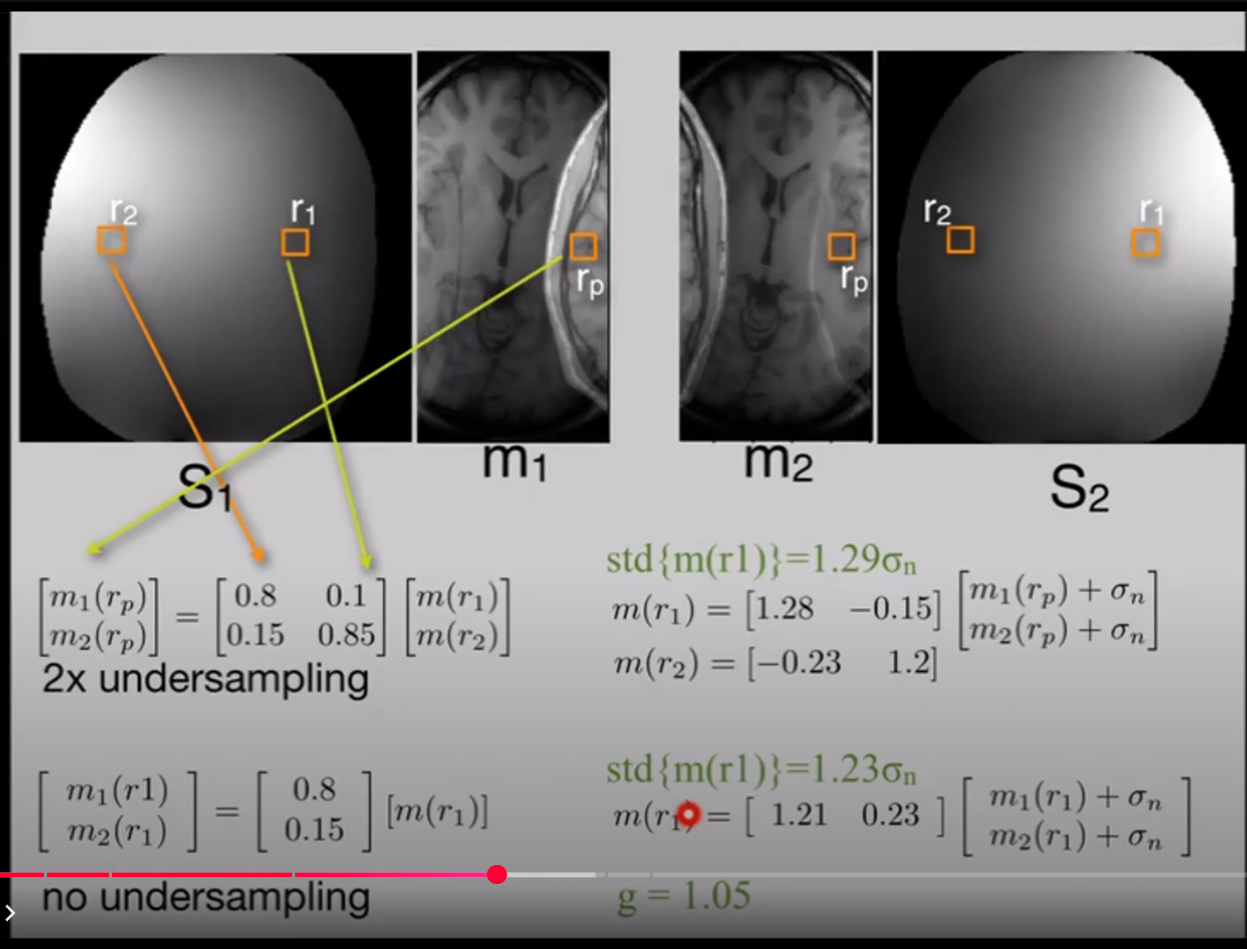
Normal Sampling
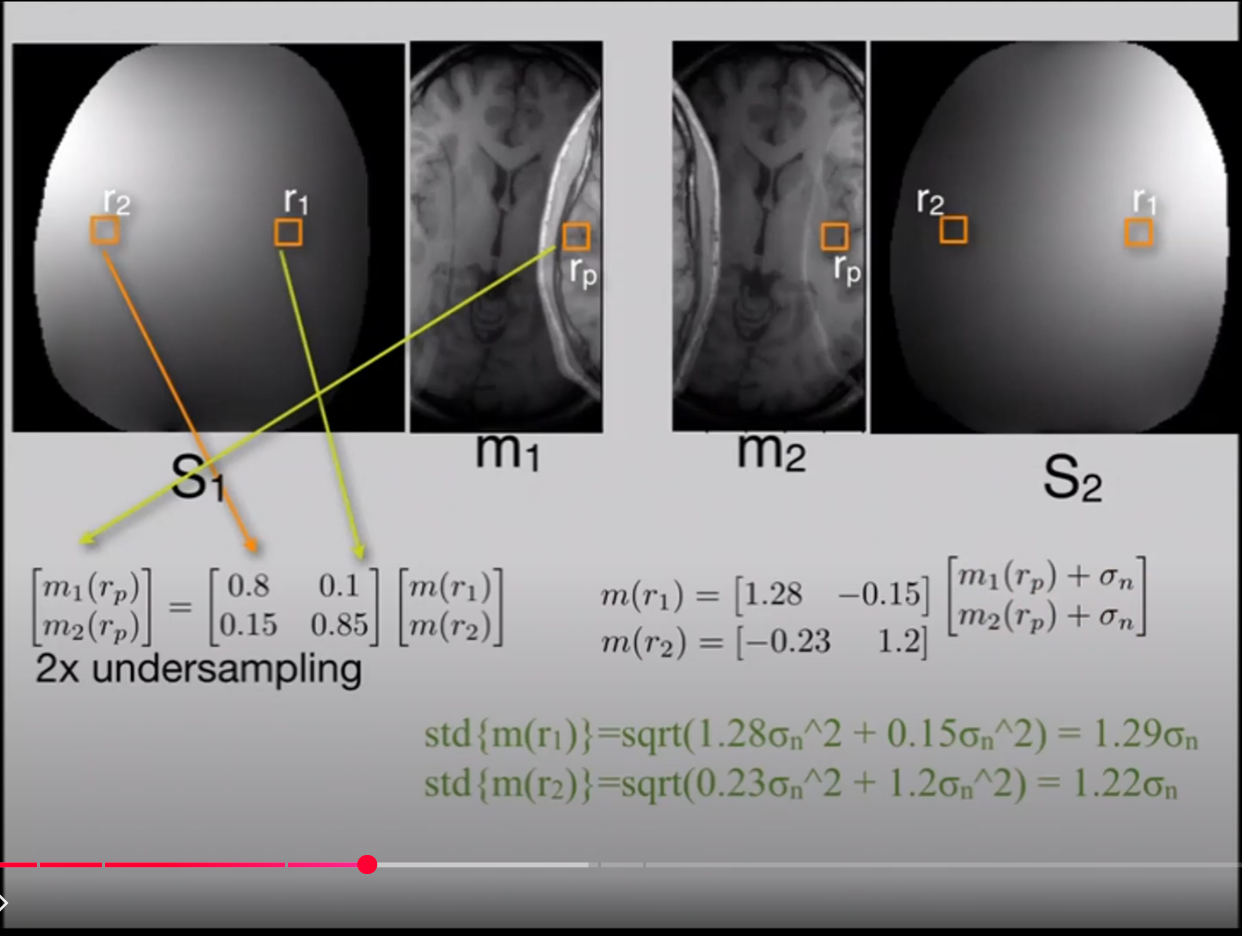
2x Undersampling

SENSE (Sensitivity Encoding) accelerates MRI by undersampling k-space, causing aliasing where signals from distinct locations ($r_1, r_2, \dots, r_R$) overlap onto a single pixel $r_p$. Coil sensitivities are used to unfold these signals.

SENSE Unfolding & Noise (R-fold Undersampling)

For $N_c$ coils and an acceleration factor $R$, the measured aliased signals $\mathbf{m}_{\text{aliased}}(r_p) \in \mathbb{C}^{N_c}$ at pixel $r_p$ are:

$$\mathbf{m}_{\text{aliased}}(r_p) = \mathbf{S}(r_p) \cdot \mathbf{m}_{\text{true}}(r_p) + \mathbf{n}(r_p)$$

Where:

  • $\mathbf{m}_{\text{true}}(r_p) = [m(r_1), m(r_2), \dots, m(r_R)]^T \in \mathbb{C}^{R}$ are the true image intensities at the $R$ aliasing locations.
  • $\mathbf{S}(r_p) \in \mathbb{C}^{N_c \times R}$ is the sensitivity encoding matrix for pixel $r_p$:
$$\mathbf{S}(r_p) = \begin{bmatrix} S_1(r_1) & S_1(r_2) & \dots & S_1(r_R) \\ S_2(r_1) & S_2(r_2) & \dots & S_2(r_R) \\ \vdots & \vdots & \ddots & \vdots \\ S_{N_c}(r_1) & S_{N_c}(r_2) & \dots & S_{N_c}(r_R) \end{bmatrix}$$

with $S_c(r_k)$ being the sensitivity of coil $c$ at location $r_k$.

  • $\mathbf{n}(r_p) \in \mathbb{C}^{N_c}$ is the noise vector.

Reconstruction involves inverting $\mathbf{S}(r_p)$ (typically via pseudo-inverse if $N_c > R$):

$$\mathbf{m}_{\text{true}}(r_p) = \mathbf{S}^{\dagger}(r_p) \cdot \mathbf{m}_{\text{aliased}}(r_p) - \mathbf{S}^{\dagger}(r_p) \cdot \mathbf{n}(r_p)$$

where $\mathbf{S}^{\dagger} = (\mathbf{S}^H \mathbf{\Psi}^{-1} \mathbf{S})^{-1} \mathbf{S}^H \mathbf{\Psi}^{-1}$ and $\mathbf{\Psi}$ is the noise covariance matrix. If noise is i.i.d. with variance $\sigma_n^2$ across coils, $\mathbf{\Psi} = \sigma_n^2 \mathbf{I}$.

Example (R=2, $N_c=2$, i.i.d. noise):
If $\mathbf{S} = \begin{bmatrix} 0.8 & 0.1 \ 0.15 & 0.85 \end{bmatrix}$, then
$\mathbf{S}^{-1} = \begin{bmatrix} 1.28 & -0.15 \ -0.23 & 1.2 \end{bmatrix}$.

The g-factor

The g-factor at a specific unfolded pixel location $r_k$ quantifies noise amplification due to the unfolding process (for undersampled SENSE) or coil combination (no undersampling).

The noise covariance of the unfolded image $\mathbf{m}_{\text{true}}$ is:

$$\text{cov}(\mathbf{m}_{\text{true}}) = \mathbf{S}^{\dagger} \cdot \text{cov}(\mathbf{n}) \cdot (\mathbf{S}^{\dagger})^H$$

If noise is i.i.d. in raw coil data ($\text{cov}(\mathbf{n}) = \sigma_n^2 \mathbf{I}$), then:

$$\text{cov}(\mathbf{m}_{\text{true}}) = \sigma_n^2 (\mathbf{S}^H \mathbf{S})^{-1}$$

The standard deviation of the $k$-th unfolded pixel $m(r_k)$ is:

$$\sigma_n \sqrt{[(\mathbf{S}^H \mathbf{S})^{-1}]_{kk}}$$

The g-factor for pixel $r_k$ is often defined as:

$$g(r_k) = \sqrt{\frac{[(\mathbf{S}^H \mathbf{S})^{-1}]_{kk} \cdot [(\mathbf{S}^H \mathbf{S})_{kk}]_{\text{no accel}} }{R}} \quad \text{or simply} \quad g(r_k) = \sqrt{([(\mathbf{S}^H\mathbf{S})^{-1}]_{kk}) \cdot \left(\sum_{c=1}^{N_c} |S_c(r_k)|^2\right)}$$

A common simplification when $N_c=R$ and noise is i.i.d. per aliased pixel measurement:

If

$$\mathbf{m}_{\text{true}} = \mathbf{S}^{-1} \mathbf{m}_{\text{aliased}}$$

and each element of $\mathbf{m}_{\text{aliased}}$ has noise std $\sigma_n$:

$$\text{std}\{m(r_k)\} = \sigma_n \sqrt{\sum_{j=1}^{R} |(\mathbf{S}^{-1})_{kj}|^2 }$$

Then:

$$g(r_k) = \sqrt{\sum_{j=1}^{R} |(\mathbf{S}^{-1})_{kj}|^2 }$$

Example (R=2, $N_c=2$, using $\mathbf{S}^{-1}$ above):

  • $g(r_1) = \sqrt{ (1.28)^2 + (-0.15)^2 } \approx 1.29 \implies \text{std}{m(r_1)} \approx 1.29 \sigma_n$
  • $g(r_2) = \sqrt{ (-0.23)^2 + (1.2)^2 } \approx 1.22 \implies \text{std}{m(r_2)} \approx 1.22 \sigma_n$

No Undersampling (Full FOV, R=1)

Signal equation for pixel $r_1$ with $N_c$ coils:

$$\mathbf{m}(r_1) = \mathbf{s}(r_1) m_{\text{true}}(r_1) + \mathbf{n}(r_1)$$

where $\mathbf{m}(r_1) = [m_1(r_1), \dots, m_{N_c}(r_1)]^T$ and $\mathbf{s}(r_1) = [S_1(r_1), \dots, S_{N_c}(r_1)]^T$.

Optimal combination (assuming i.i.d. noise $\sigma_n$ per coil):

$$m_{\text{true}}(r_1) = \frac{\mathbf{s}(r_1)^H \mathbf{m}(r_1)}{\|\mathbf{s}(r_1)\|_2^2}$$

The variance is:

$$\sigma_{m(r_1)}^2 = \frac{\sigma_n^2}{\|\mathbf{s}(r_1)\|_2^2}$$

The g-factor is:

$$g(r_1) = \frac{\sigma_n / \|\mathbf{s}(r_1)\|_2}{\sigma_n / \sqrt{\sum_c |S_c(r_1)|^2}} = 1$$

Often, $g \approx 1$ for no undersampling, reflecting optimal coil combination. Example value $g=1.05$ might account for practical factors or a different noise reference.

Interpretation & Influencing Factors

  • $g \approx 1$: Minimal noise amplification
  • $g > 1$: Noise amplified, local SNR reduced. $\text{SNR} \propto \frac{1}{g\sqrt{R}}$

Factors influencing g (SENSE):

  1. Coil Geometry: Distinct sensitivity profiles $\implies$ lower $g$
  2. Acceleration Factor (R): Higher $R \implies$ generally higher $g$
  3. Pixel Location: $g$ is spatially varying
  4. Regularization: Can affect effective $g$

Lower g-factors are desirable for better image quality.